神经网络之反向传播算法
之前使用神经网络算法的时候并没有认真总结关键的算法,虽然可以用但总觉得不爽,于是这两天对神经网络算法中的反向传播(Back Propagation)进行了推导。即理解了算法的数学本质,也对神经网络算法的工程特性有了深刻体会,工程算法真的是以解决问题为驱动的,追求的是解决问题的实用性。
神经网络
网络拓扑
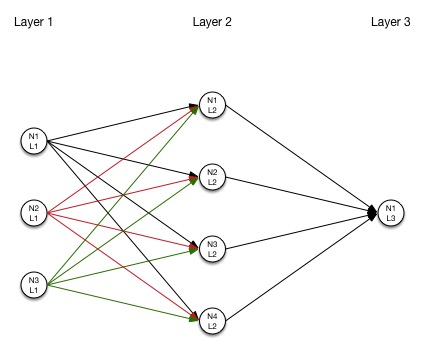
神经元
神经元是神经网络的基本构成,上图的每一个圆圈代表了一个神经元。每一个神经元有一个输入和一个输出,神经元的作用是对输入值进行计算。下图是一个神经元的简单示意图:
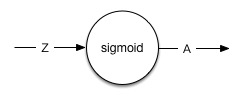
- 该神经元的输出:$ a=f(z)=sigmoid(z) $
神经元输入
在一个复杂点的神经网络中,一个神经元接收来自多个前级神经元的激活输出,并进行加权相加后产生该神经元的输入值,这个过程示意图如下:
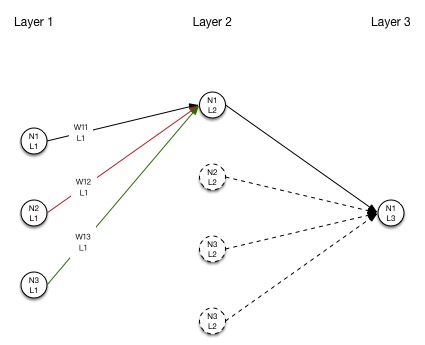
定义第 $ l^{th} $ 层第 $ j^{th} $ 个神经元的输入:
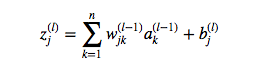
神经元加权
神经元的加权结构可以看下面的示意图:
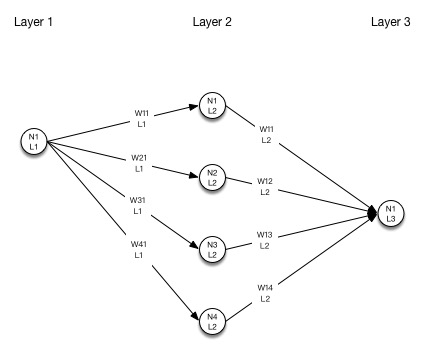
注,第一层神经元的输入就是采样数据,不需要计算z值,这层采样数据直接通过权重计算输入到第二层的神经元。
反向传播算法
代价函数
定义代价函数:$ cost = {1 \over 2} \sum (y^{(i)} - a^{(i)})^2 $
神经元错误量 $ \delta_j^{(l)} $
每个神经元的输入记为’z’,经过激活函数’f(z)‘生成激活值’a’,通常情况下激活函数使用sigmoid()。那么假设对于每个神经元的输入’z’做一点微小的改变记为 $ \Delta z $,由这个改变引起的代价变化记为这个神经元的错误量 $ \delta_j^{(l)} $,从这个定义可以看出来这是一个代价函数相对于神经元的输入’z’的偏导数。
定义 $ \delta_j^{(l)} $ 为 $ l^{th} $ 层中的第 $ j^{th} $ 个神经元的错误量,记作:$ \delta_j^{(l)} =\frac{\partial C}{\partial z_j^{(l)}} $
经过数学推导可以得出结论:
- 最后一层(L层)第j个神经元的错误量:
$$ \delta_j^{(L)} = -(y-a_j^{(L)}) \bigodot [a_j^{(L)}(1-a_j^{(L)})] $$
简单推导若成如下:
$$ \delta_j^{(L)} = \frac{\partial C}{\partial z_j^{(l)}} $$
$$ \frac{\partial C}{\partial z_j^{(l)}} = \frac{\partial C}{\partial a_j^{(L)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} $$
$$ \frac{\partial C}{\partial a_j^{(L)}} \frac{\partial a_j^{(L)}}{\partial z_j^{(L)}} = -(y-a_j^{(L)}) \bigodot [a_j^{(L)}(1-a_j^{(L)})] $$
y:采样的结果
$ a_j^{(L)} $:样本输入计算的结果
- 其余各层(l层)第j个神经元的错误量:
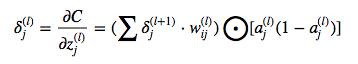
因为首先可以算出来每一层的激活量 $ a_j^{(l)} $,那么可以看出来除了最后一层外的其他层的错误量可以靠后面一层的错误量计算出来,直至推算到最后一层 $ \delta_j^{(L)} $。
因此反向传播算法也就是从最后一层往前一层一层计算的过程,与计算激活量的方向正好相反,因此得名反向传播。
权重调整及偏置调整
观察每个神经元的输入可以发现神经网络计算过程中最重要的是要确定两个量权重w和偏置b。
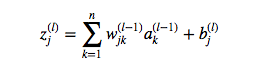
仿照错误量计算方法将问题进行一下转化,是否可以计算出代价函数相对于权重和偏置的变化速率(偏微分),然后通过乘以一个小数字(学习速率)来一点一点降低代价函数的输出,从而逼近最终需要的权重及偏置值呢?
因此可以将问题转化为求 $ \frac{\partial C}{\partial w_{jk}^{(l)}} $ 和 $ \frac{\partial C}{\partial b_j^{(l)}} $
通过推导可以得出:
$$ \frac{\partial C}{\partial w_{jk}^{(l)}} = \delta_j^{(l+1)} a_k^{(l)} $$
$$ \frac{\partial C}{\partial b_{jk}^{(l)}} = \delta_j^{(l)} $$
基于前面对于错误量 $ \delta_j^{(l)} $ 就可以非常简单的得到相应的结果。
那么最终对于权重及偏置的调整可以这样做:
$$ w = w-\eta \frac{\partial C}{\partial w_{jk}^{(l)}} $$
$$ b = b-\eta \frac{\partial C}{\partial b_{jk}^{(l)}} $$
其中 $ \eta $ 是一个非常小的正数,这个数字也被叫做“学习速率”,通过这个值的调整可以控制拟合的速度。
推导过程
- 前面的部分直接使用了结论,实际推到过程比较啰嗦,markdown直接编写公式也不方便,索性把推到过程的草稿贴出来参考好了
:-)
实验代码
做一个简单的神经网络实验,网络设计为3层,第一层对应3个输入,第二层用4个神经元,第三层为输出层使用1个神经元。
网络初始化过程如下:
# network design:
# input(layer_1): 3 nodes
# weights: 3x4 matrix
# layer_2: 4 nodes
# weights: 4x1 matrix
# output: 1 node
# create training data
input = np.array([[0, 0, 1],
[0, 1, 0],
[0, 1, 1],
[1, 0, 0],
[1, 0, 1]])
# create the label related with the input training data
output = np.array([[0],
[1],
[0],
[1],
[1]])
# initialize random weight
weight_layer_1 = np.random.rand(3, 4)
weight_layer_2 = np.random.rand(4, 1)
训练过程主要代码:
# x/y is for drawing chart
x=[]
y=[]
# learning rate
eta = 0.1
loop = 0
while loop < 50000:
# feed forward calculation
z_layer_2 = np.dot(input, weight_layer_1)
a_layer_2 = sigmoid(z_layer_2)
z_layer_3 = np.dot(a_layer_2, weight_layer_2)
a_layer_3 = sigmoid(z_layer_3)
if loop % 100 == 0:
# calculate the cost
c = cost(output, a_layer_3)
print "[%d] Cost: %f" % (loop, c)
print "Perception: ", a_layer_3
x.append(loop)
y.append(c)
loop += 1
# back propagation
# calculate delta_3
delta_layer_3 = cost_derivative(output, a_layer_3)*deriv_z(a_layer_3)
# calculate delta_2
delta_layer_2 = np.dot(delta_layer_3, weight_layer_2.T)*deriv_z(a_layer_2)
# there is NO delta_layer_1, since layer1 is the input layer
# calculate new weight for layer 2
weight_layer_2 -= eta*np.dot(a_layer_2.T, delta_layer_3)
# calculate new weight for layer 1
weight_layer_1 -= eta*np.dot(input.T, delta_layer_2)
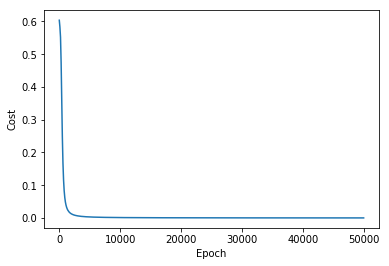
上面代码可以观察到每100次计算修正后的代价函数输出以及预测值,可以发现代价值在逐渐趋近于0,说明误差在降低,预测值越来越接近实际采样的数值。
为了更加清晰的看到这个过程,把x/y输出在图上进行查看,可以观察到拟合过程,并且可以看到拟合的速度变化情况。
import matplotlib.pyplot as plt
plt.plot(x, y)
plt.xlabel("Epoch")
plt.ylabel("Cost")
plt.show()
参考
https://www.youtube.com/watch?v=mOmkv5SI9hU&list=PLLssT5z_DsK-h9vYZkQkYNWcItqhlRJLN&index=52
