目录

3D 设计软件和游戏中的图像经常是以一个观测者的角度展示的，可以把这个过程想象成一个人拿着一台摄像机在拍摄，在机器视觉中叫摄像机模型。

研究过程中基于 OpenCV 做了一个简单实现，项目代码可以在这里下载到 “github 代码下载”，欢迎大家下载交流。

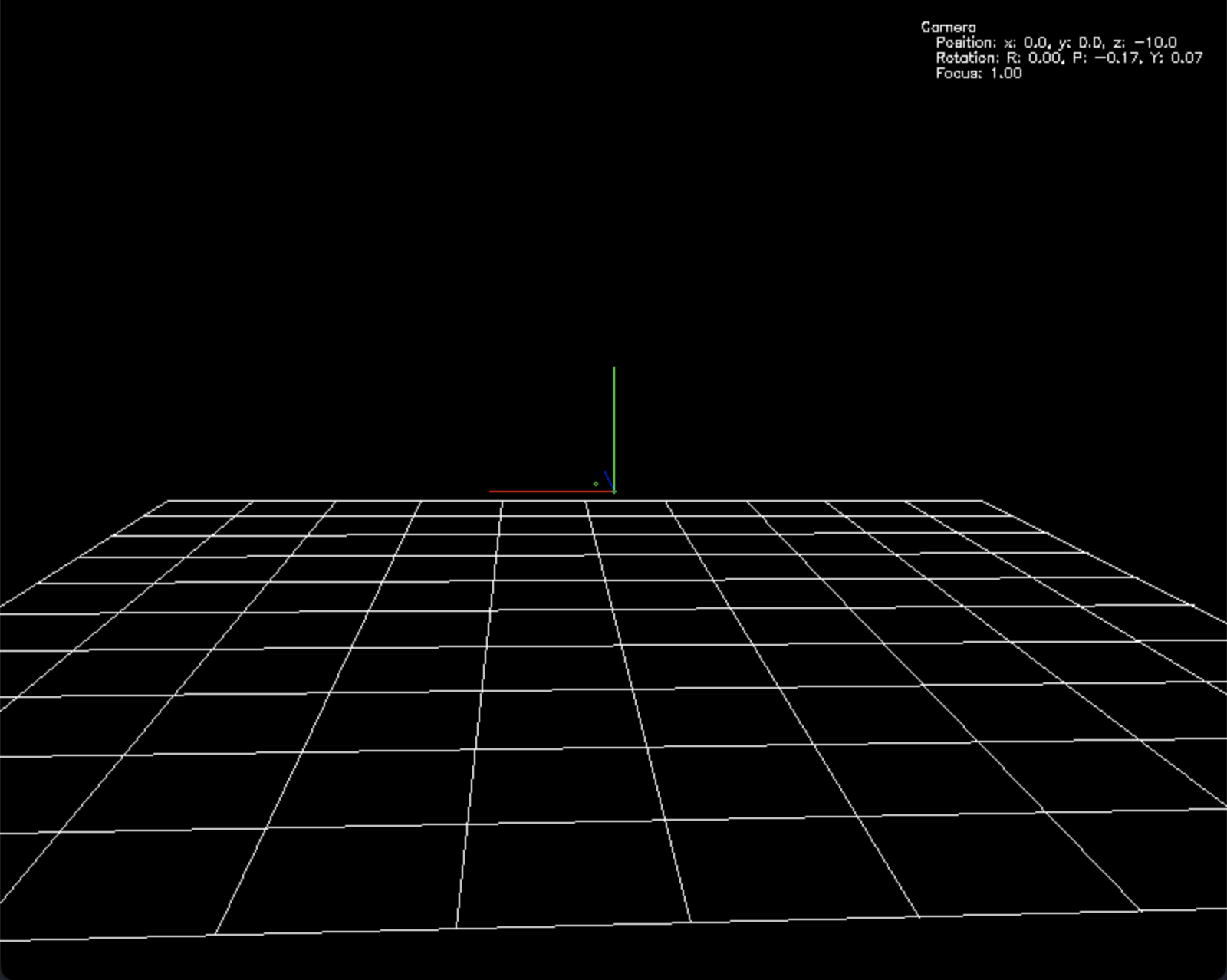
摄像机模型的数学模型

座标系

理解摄像机模型需要建立对应的座标系，在这个模型里面涉及到了下面 3 个座标系：

• 世界座标系 (World frame)

  被观测目标存在于世界座标系中，使用世界座标系座标表示位置，是个 3 维座标系，可以使用常用的单位，比如‘米’。

• 相机座标系 (Camera frame)

  通常使用摄像机的光学中心为原点，是一个 3 维座标系，表示从相机的光学中心原点来衡量各个目标的位置，尺度可以保持和世界座标系统一，比如都使用‘米’；相机可以移动到世界座标系中的任意位置和任意角度（姿态）。

• 像平面座标系 (Image plane frame)

  这是最终观测的图像座标系，是一个 3 维座标系，在相机中是 CCD 的座标系，例如以左上角为原点，尺度为‘像素’。

座标转换

当移动摄像机时，摄像机成像的结果可以通过座标转换来完成：

1. 把世界座标系中的物体座标进行’座标系变换’，转换成相机座标系中的座标
2. 通过相机内参转换到像平面座标系

座标系变换过程

世界座标 $O_w$ 用下面形式表示:

$$ \left( \begin{matrix} X_w
Y_w
Z_w \end{matrix} \right) $$

摄像机在世界座标系中被移动到 $t$ 位置：

$$ \left( \begin{matrix} x_t
y_t
z_t \end{matrix} \right) $$

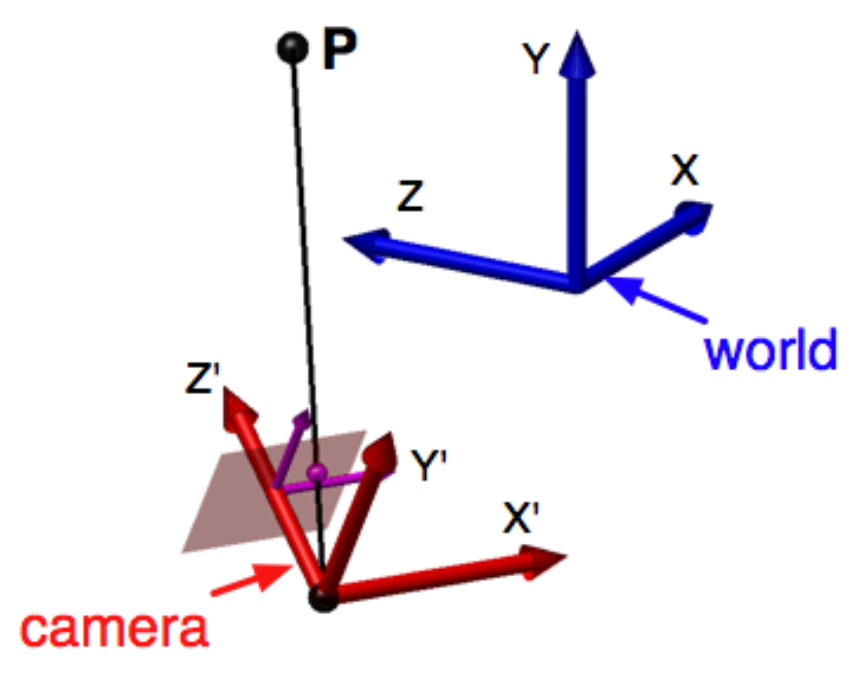
第一步：先抵消掉摄像机的空间移动 $t$，也就是 $O_w - t$。这一步后新的座标系与摄像机座标系原点重叠。

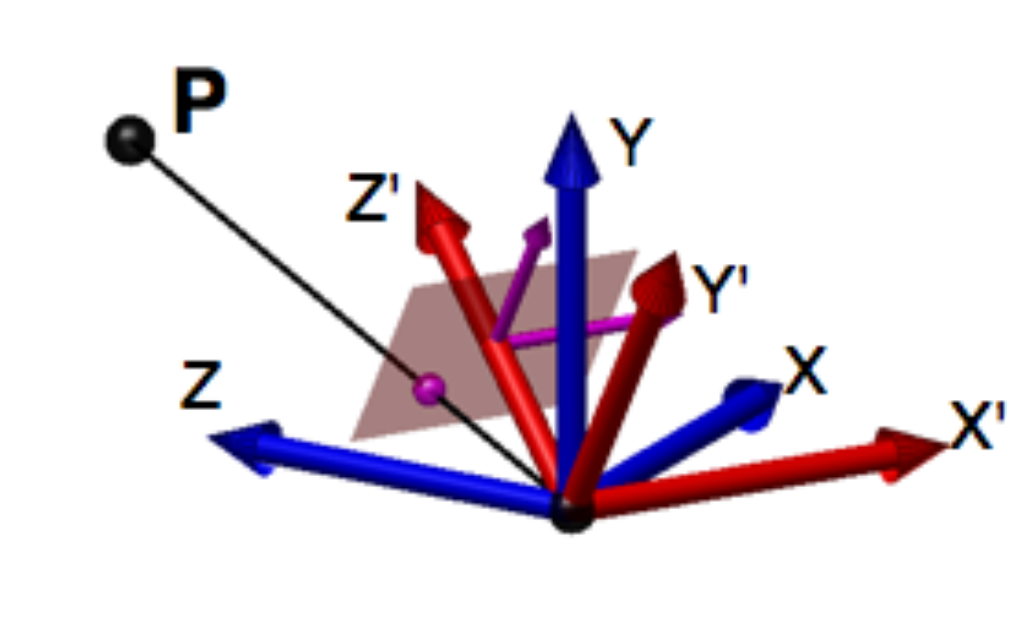
第二步：旋转座标系第一步后的新座标系到摄像机座标座标系，旋转矩阵 $R$ ，关于座标旋转参见旋转矩阵，完成旋转后得到了摄像机座标系下的座标 $O_c$

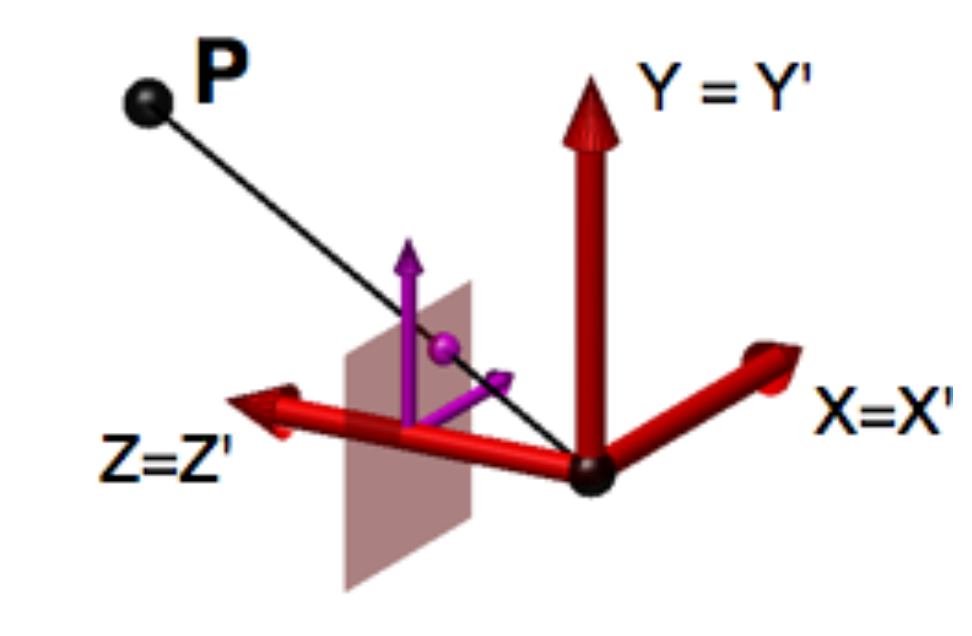
相机座标转化到像平面座标

先看一下小孔成像模型，使用虚拟像平面可以把座标转换简化。

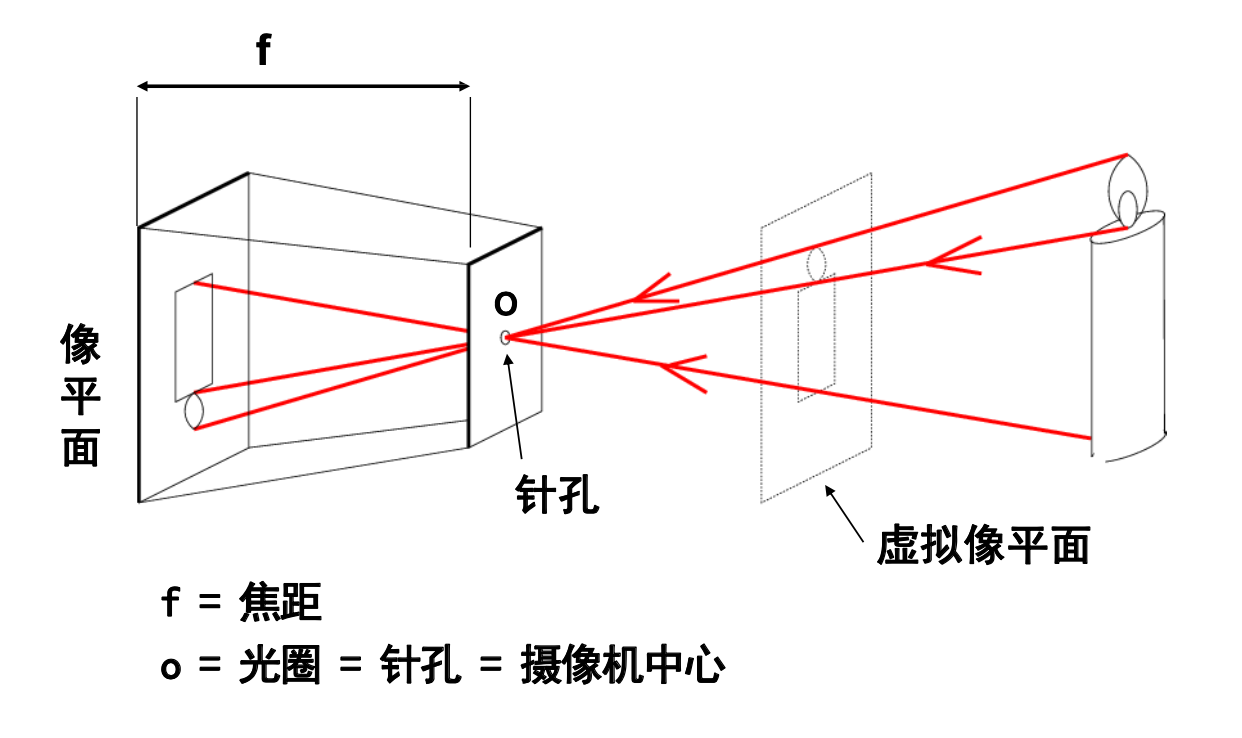
简化后的模型如下图：

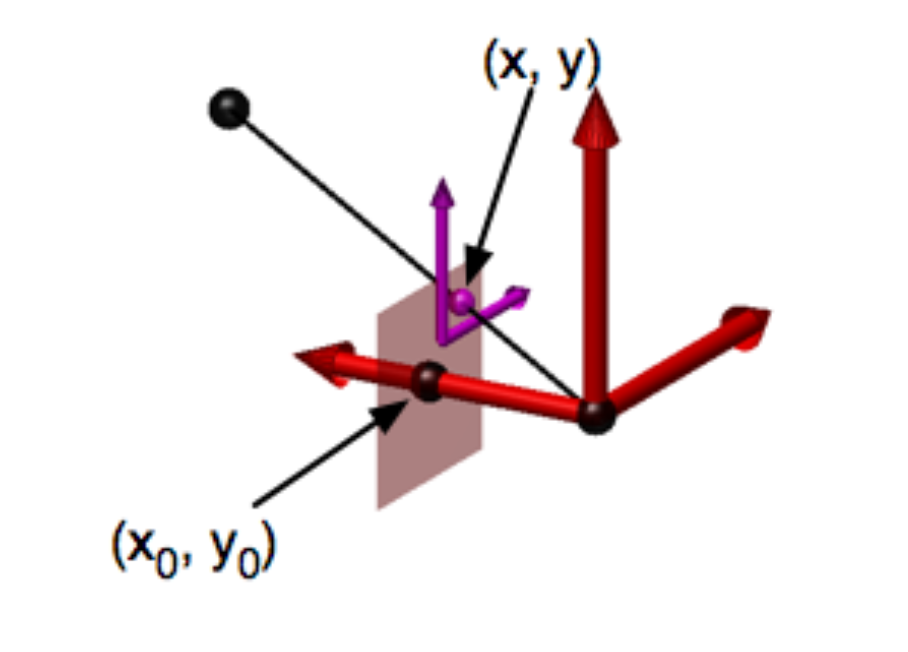
摄像机座标系与虚拟像平面交于点 $(x_o, y_o)$，摄像机座标系下的点 $O_c$ 在虚拟像平面上的投影点是 $(x’, y’)$

通过相似三角形可以容易得到：$ x’ \over X_c $ = $ y’ \over Y_c $ = $ f \over Z_c $，也就是：

$$ x‘ = f \frac {X_c} {Z_c} $$ $$ y’ = f \frac {Y_c} {Z_c} $$ $$ z‘ = f \frac {Z_c} {Z_c} $$

在摄像机虚拟像平面座标系下（左上角为原点，像素为单位），摄像机座标系与虚拟像平面的交点像素座标为 $(x_o, y_o)$，摄像机座标系下的点 $O_c$ 在虚拟像平面上投影点像素级座标是 $(x, y)$，摄像机 CCD 的像素点在 x 和 y 轴方向上的排列密度为 $\sigma_x$ （单位：pixels/meter）和 $\sigma_y$ （单位：pixels/meter），那么：

中间式子可以写成下面形式：

通过逆矩阵运算得到：

再把第一个矩阵拆成下面的形式：

再做矩阵逆运算得到：

摄像机数学模型

现在已经有了一个摄像机的数学模型：

第一步：把观察目标从世界坐标旋转到摄像机坐标

第二步：把摄像机坐标转换到摄像机虚拟像平面像素坐标

实现一个摄像机模型

第一步：世界坐标系到相机坐标系转换

根据摄像机旋转角度计算出旋转矩阵 R：

      def rotate(self, roll, pitch, yaw):
          '''
          Rotate camera by roll, pitch, yaw
          '''
          rx, _ = cv2.Rodrigues((pitch, 0, 0))
 Rodrigues(src, dst=None, jacobian=None, /) -> dst, jacobian                                                                            

被观测物体的世界坐标转换到相机坐标：

      def trans_to_cam(self, v):
          '''
          Transform the world coordinate vertices to camera coordinate vertices
              v: vertices in world coordinate frame
          '''
          vc = np.dot(self.R, (v.T - np.array([[self._x], [self._y], [self._z]])))
          return vc.T

第二步：把相机坐标投影到相机虚拟像平面上

定义相机内参：包括焦距、CCD像素密度参数，写出相机内参矩阵

          # camera focus length in meter
          self._f = 1

          # scale factor: pixels/meter
          self._s = 800
          
          # camera intrinsic matrix
          self.intrinsic = np.array([[self._f*self._s,    0,                  self._canvas_width/2.0],
                                     [0,                  self._f*self._s,    self._canvas_height/2.0],
                                     [0,                  0,                  1]])

进行投影转换计算。注：由于程序实现时世界/相机坐标系采用的是右手Z轴向前的形式，因此计算结果多了一步转换的运算。

      def project(self, v):
          '''
          Project the vertices of camera coordinate to camera image plane coordinate
              v: vertices in camera coordinate frame
                  u = width - f*(Y/X)
                  v = height - f*(Z/X)
          '''
          Z = np.expand_dims(v[:, -1], axis=1)
          proj_v = np.dot(self.intrinsic, v.T) / Z
          proj_v = proj_v.T
          proj_v[:, 0:2] = [self._canvas_width, self._canvas_height] - proj_v[:, 0:2]
          return proj_v[:, :2]

Demo：

参考

• CS231A 鲁鹏
• DD2429 from KTH