目录
计算机图形学中的仿射变换包括平移、缩放、旋转等,在机器人位置描述的时候也需要使用到平移、旋转。这里主要介绍旋转的处理方法。
先举个简单例子
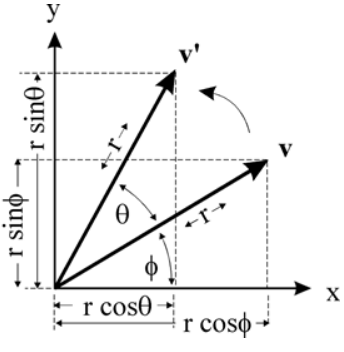
设想一个二维平面空间里的“一个点”状机器人的简单情况,最初机器人位于平面直角坐标系中的 (1, 0) 点,先让机器人围绕着原点旋转角度 $\phi$ ,那么机器人的新的位置坐标可以很容易的用以下方式来表示:
$$ (cos(\phi), sin(\phi)) $$
让机器人再从刚才的位置继续旋转 $\theta$ 角,那么机器人的新的位置坐标也很直观的用下面式子表示:
$$ (cos(\phi+\theta), sin(\phi+\theta)) $$
复杂一点的例子
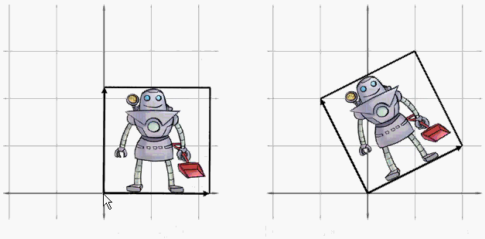
在平面直角坐标系下,如果机器人不再是一个简单的点而是一个平面,那么机器人躯干中的任意一个点 (x, y) 经过旋转后在原平面直角坐标系下的新坐标是什么?
旋转矩阵
二维平面直角坐标系旋转矩阵推导

机器人躯干上的任意点 (x, y) 对应向量 v,旋转 $\theta$ 后的位置计作 (x’, y’)对应新的向量 v’。
那么:
$$
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)=
\left(
\begin{matrix}
r*cos(\phi) \\
r*sin(\phi)
\end{matrix}
\right)
$$
$$
\left(
\begin{matrix}
x' \\
y'
\end{matrix}
\right)=
\left(
\begin{matrix}
r*cos(\phi+\theta) \\
r*sin(\phi+\theta)
\end{matrix}
\right)
$$
三角和差化积公式:
$$ cos(\phi+\theta) = cos(\phi)*cos(\theta) - sin(\phi)*sin(\theta) $$
$$ sin(\phi+\theta) = sin(\phi)*cos(\theta) + cos(\phi)*sin(\theta) $$
带入和差化积公式后:
$$
\left(
\begin{matrix}
x' \\
y'
\end{matrix}
\right)=
\left(
\begin{matrix}
r*cos(\phi)*cos(\theta) - r*sin(\phi)*sin(\theta) \\
r*sin(\phi)*cos(\theta) + r*cos(\phi)*sin(\theta)
\end{matrix}
\right)=
\left(
\begin{matrix}
x*cos(\theta) - y*sin(\theta) \\
y*cos(\theta) + x*sin(\theta)
\end{matrix}
\right)
$$
用矩阵的方法书写上面的公式:
$$
\left(
\begin{matrix}
x' \\
y'
\end{matrix}
\right)=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) \\
sin(\theta) & cos(\theta)
\end{matrix}
\right)*
\left(
\begin{matrix}
x \\
y
\end{matrix}
\right)
$$
旋转矩阵 ‘R’:
$$
R=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) \\
sin(\theta) & cos(\theta)
\end{matrix}
\right)
$$
二维平面之交坐标系旋绕任一点旋转
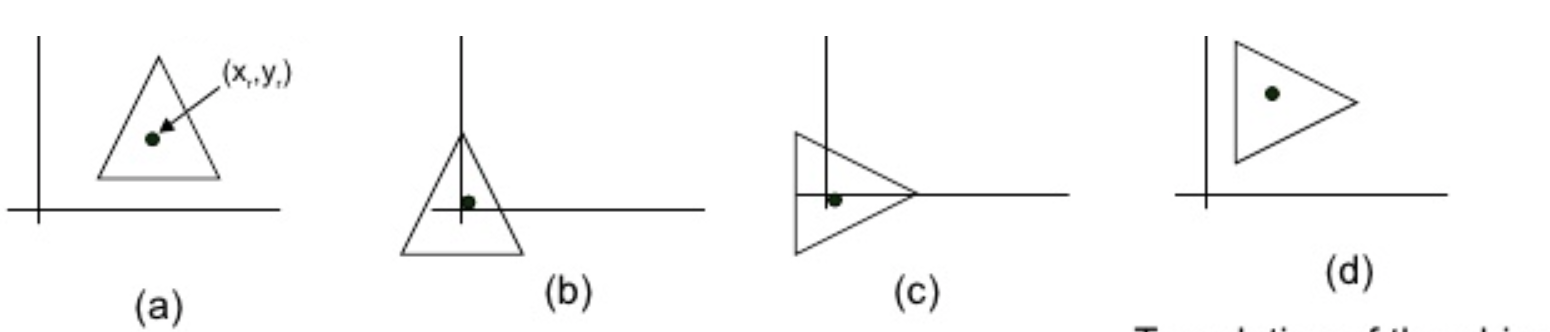
思路如下:
- 步骤 (a):找到旋转点在原坐标系中的坐标 (x, y)
- 步骤 (b):把坐标系平移到(x,y)后重新计算新的坐标
- 步骤 ©:对新的坐标进行旋转
- 步骤 (d):把结果进行反向平移
思考:平移是否可以用矩阵进行计算呢,如果可以的话会有什么好处呢?
平移矩阵
- 平移: 把任意点 (x, y) 平移 (tx, ty) 的到新的点 (x’, y’)
$$ x’ = x + tx $$
$$ y’ = y + ty $$
使用齐次坐标进行矩阵表达:
$$
\left(
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right) =
\left(
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right) *
\left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
$$
所以,平移可以通过平移矩阵来表示。
$$
\left(
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right)
$$
如何用矩阵的形式表示绕任意点旋转呢?
$$
\left(
\begin{matrix}
1 & 0 & -tx \\
0 & 1 & -ty \\
0 & 0 & 1
\end{matrix}
\right)
$$
- 第二步:使用旋转矩阵进行旋转。注意,这里需要使用齐次矩阵
$$
R=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0 \\
0 & 0 & 1
\end{matrix}
\right)
$$
$$
\left(
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right)
$$
整体如下:
$$
\left(
\begin{matrix}
1 & 0 & tx \\
0 & 1 & ty \\
0 & 0 & 1
\end{matrix}
\right) *
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0 \\
0 & 0 & 1
\end{matrix}
\right) *
\left(
\begin{matrix}
1 & 0 & -tx \\
0 & 1 & -ty \\
0 & 0 & 1
\end{matrix}
\right)=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) & (1-cos(\theta))*tx + sin(\theta)*ty \\
sin(\theta) & cos(\theta) & (1-cos(\theta))*ty - sin(\theta)*tx \\
0 & 0 & 1
\end{matrix}
\right)
$$
利用上面的旋转平移矩阵可以很方便的计算出 x’ 和 y’
$$
\left(
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right) =
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) & (1-cos(\theta))*tx + sin(\theta)*ty \\
sin(\theta) & cos(\theta) & (1-cos(\theta))*ty - sin(\theta)*tx \\
0 & 0 & 1
\end{matrix}
\right) *
\left(
\begin{matrix}
x \\
y \\
1
\end{matrix}
\right)
$$
$$
\left(
\begin{matrix}
x' \\
y' \\
1
\end{matrix}
\right) =
\left(
\begin{matrix}
x*cos(\theta) - y*sin(\theta) + (1-cos(\theta))*tx + sin(\theta)*ty \\
x*sin(\theta) + y*cos(\theta) + (1-cos(\theta))*ty - sin(\theta)*tx \\
1
\end{matrix}
\right)
$$
三维旋转矩阵
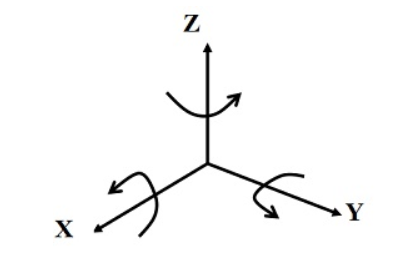
绕 X 轴转 $\theta$ 的旋转矩阵:
$$ x’ = x $$
$$
\left(
\begin{matrix}
y' \\
z'
\end{matrix}
\right)=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) \\
sin(\theta) & cos(\theta)
\end{matrix}
\right)*
\left(
\begin{matrix}
y \\
z
\end{matrix}
\right)
$$
$$
\left(
\begin{matrix}
x' \\
y' \\
z'
\end{matrix}
\right)=
\left(
\begin{matrix}
1 & 0 & 0 \\
0 & cos(\theta) & -sin(\theta) \\
0 & sin(\theta) & cos(\theta)
\end{matrix}
\right)*
\left(
\begin{matrix}
x \\
y \\
z
\end{matrix}
\right)
$$
因此:
$$
R=
\left(
\begin{matrix}
1 & 0 & 0 \\
0 & cos(\theta) & -sin(\theta) \\
0 & sin(\theta) & cos(\theta)
\end{matrix}
\right)
$$
绕 Y 轴转 $\theta$ 的旋转矩阵:
$$
R=
\left(
\begin{matrix}
cos(\theta) & 0 & sin(\theta) \\
0 & 1 & 0 \\
-sin(\theta) & 0 & cos(\theta)
\end{matrix}
\right)
$$
绕 Z 轴转 $\theta$ 的旋转矩阵:
$$
R=
\left(
\begin{matrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0 \\
0 & 0 & 1
\end{matrix}
\right)
$$
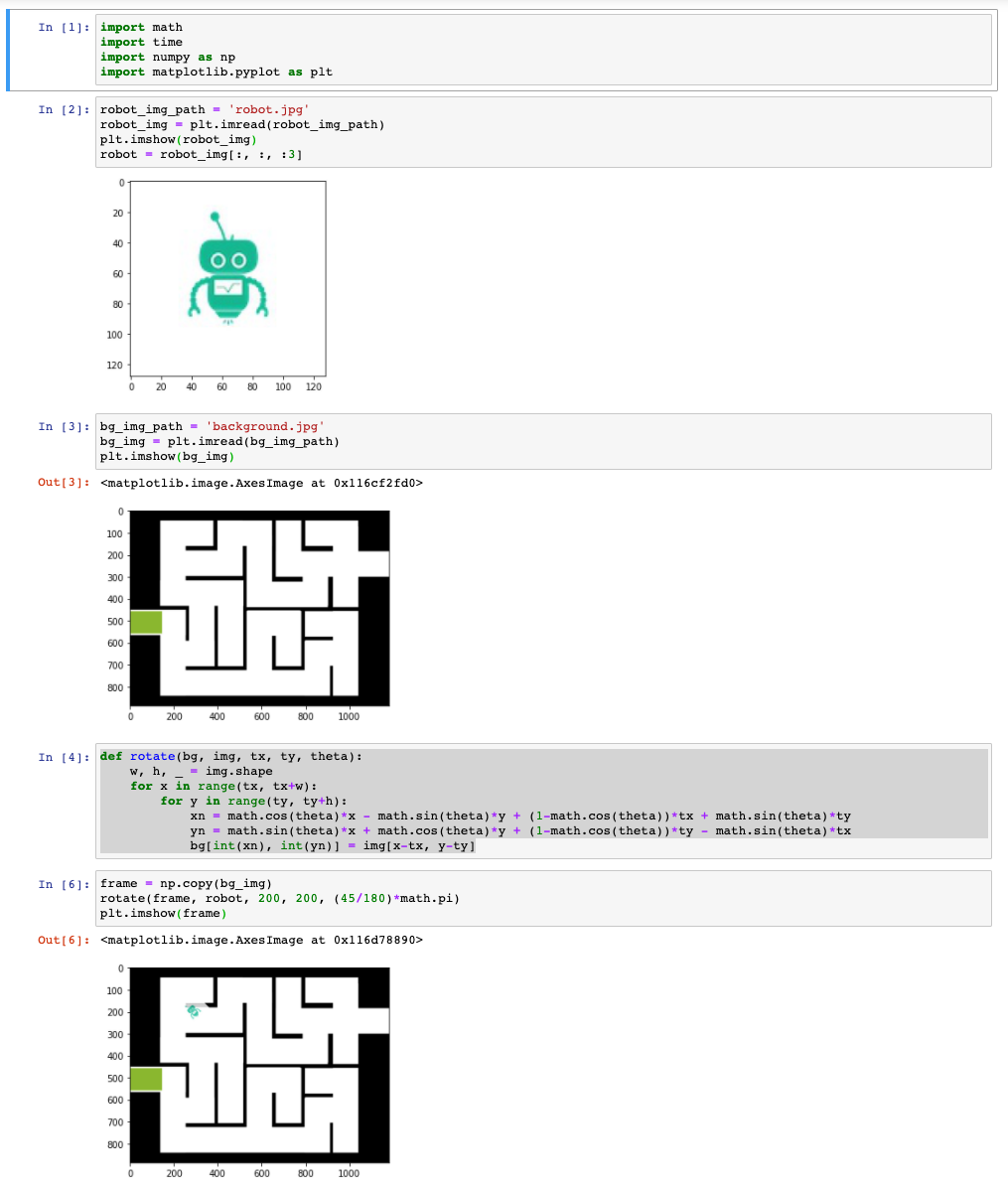
代码实验