sigmoid激活函数在神经网络中有着强大的通用性，但也存在这一些问题，比如：

1. 在w/b参数还没有训练成熟时，训练预测偏差较大，此时的训练速度会较慢。这个问题的解决方法有两种：
   • 使用交叉熵代价函数: $ C = -{1\over n} \sum_{i=1}^n [y_i \ln a_i + (1-y_i) \ln (1-a_i)] $
   • 使用softmax和log-likelyhood代价函数作为输出层
2. sigmoid的输出结果是伯努利分布 $ P(y_1|X), P(y_2|X), … P(y_n|X) $，说明每一个输出项之间是相互独立的，这在预测一种输出结果的情形时不太符合人们的直观感受。这个问题也可以用softmax输出层解决，因为softmax的输出是多项分布：$ P(y_1, y_2, … y_n | X) $，其中y1, … yn之间相互关联，且总和为1。

这样看起来softmax是个很有效的方法，下面就对这个方法进行一些研究。

softmax定义：

将softmax层应用在网络输出层时，每一个神经元的softmax激活输出可以理解为该神经元对应结果的预测概率，这里有几个基本事实：

• 每个神经元的输出为正数，并且输出数值介于0-1之间。
• 所有神经元的输出总和为1。
• 某一项输入（Z值）增大时，其对应的输出概率增大；同时其他输出概率同时减小（总和总是1）。该结论可以从$ \frac {\partial a_i} {\partial {z_i}} $（总为正数）以及$ \frac {\partial a_i} {\partial {z_j}}$（总为负数）推算出来，这两个数字也说明了softmax的输入／输出单调性。
• softmax的每个激活输出值之间相互关联，表现出了输出非局部性特征。直观的理解就是因为所有激活输出的总和总是为1，那么其中一个激活输出的值发生变动的时候其他的激活输出也必将变化。这一点也是跟sigmoid激活函数的很不同的一点，也说明了$ \frac {\partial a_i} {\partial {z_j}}$值存在的意义。

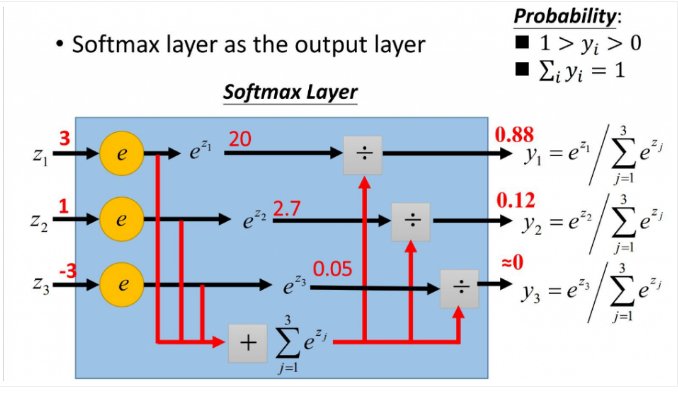
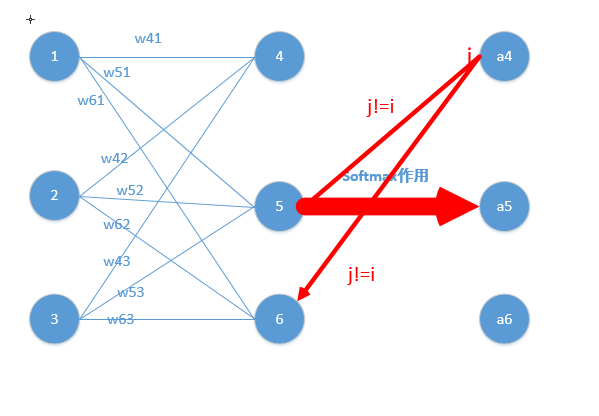
下图展示了softmax层工作的基本原理。

应用场景：

从softmax的定义知道所有输出神经元的总和为1，因此softmax可以用在预测在多种可能性中只有一个结果的场景，比如mnist手写判定。

softmax输出层组成的神经网络

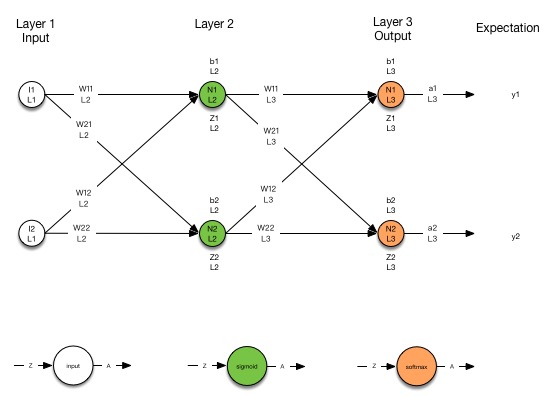
下面的图展示了一个简单的softmax输出层神经网络，中间层依然使用sigmoid。

代价函数C

为了解决在学习过程中出现的速度问题使用log-likelihood代价函数，函数定义为：

$$ C=-\sum_i^m y_i \ln a_i $$

关于实际应用这个等式需要解释一下。假设softmax输出层有4个输出，预测a值为(0.1, 0.2, 0.3, 0.4)，实际结果y为(0, 1, 0, 0)，那么这个等式为 $C = -(0\ln(0.1) + 1\ln(0.2) + 0\ln(0.3) + 0\ln(0.4))$，可以看出来因为0的存在可以让这个等式只保留实际结果为真（1）的项。这时可以把等式简化为：

$$ C=-\ln a_i | y_i=1 $$

用反向传播进行梯度下降

反向传播算法要求几个关键值：

• $ \delta_i^L $
• $ \frac {\partial C}{\partial w_{ij}^L} $
• $ \frac {\partial C}{\partial b_{i}^L} $

如果输出层使用softmax时，最后一层（L层）的相应值与使用sigmoid的情况有些不同，下面对使用softmax是的这3个值进行推导。

求解$ \delta_i^L = ({a_i^L} - y_i) $

过程如下：

求$ \frac {\partial C}{\partial w_{ij}^L} = ({a_i^L}-{y_i}){a_j^{L-1}} $的过程：

求$ \frac {\partial C}{\partial b_{i}^L} = ({a_i^L} - y_i) $的过程：

以上求解过程中用了两个重要的计算等式:

• $ \frac {\partial a_i} {\partial {z_i}} = a_i \cdot (1- a_i) $
• $ \frac {\partial a_j} {\partial {z_i}} = -{a_i \cdot a_j} | i \neq j$

下面对这两个等式进行推导：

求导情况1: $ \frac {\partial a_i} {\partial {z_i}} = a_i \cdot (1- a_i) $

• 结论：

$$ \frac {\partial a_i} {\partial {z_i}} = a_i \cdot (1- a_i) $$

• 推导过程：

求导情况2: $ \frac {\partial a_j} {\partial {z_i}} = -a_i \cdot a_j$

• 结论：

$$ \frac {\partial a_j} {\partial {z_i}} = -a_i \cdot a_j$$

• 推导过程：

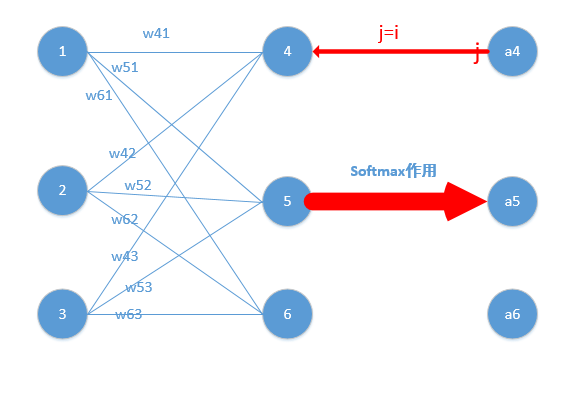
sigmoid隐藏层与softmax输出层网络

按照下图的拓扑构成的网络使用sigmoid进行隐藏层计算，使用softmax进行输出层计算，那么怎么进行网络训练呢？其实方法一样都是按照前馈网络计算代价值进行评估，使用反向传播算法进行梯度下降。

前馈网络计算步骤：

1. 在隐藏层的计算时使用sigmoid
2. 在最后输出层使用softmax

反向传播计算步骤：

• 计算输出层，计算最后一层softmax输出层的下列值：

• 计算隐藏层，反向一层一层计算sigmoid隐藏层的下列值：

计算过程中可以发现只有最后一层的$ \delta_i^L$计算较为特殊，计算权重和偏置的方法与之前的sigmoid构成的网络一致。

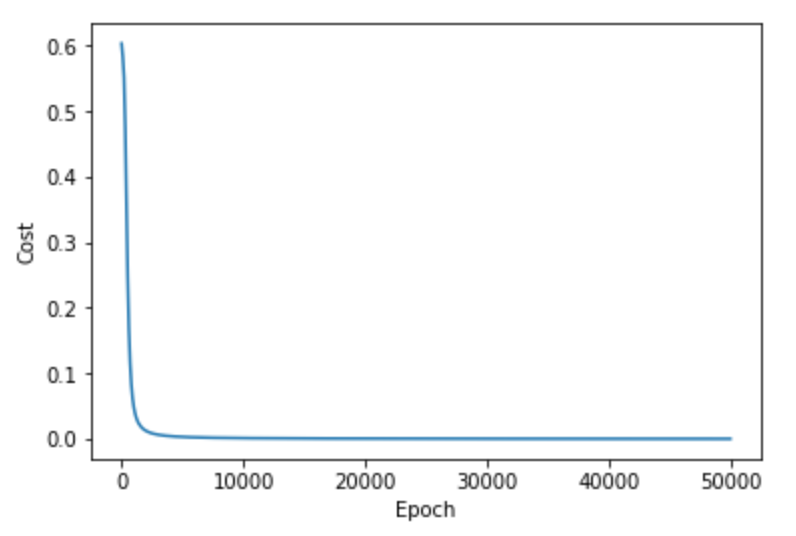
代码实例

下面的例子实验一个输入层有4个输入，隐藏层有5个神经元并且使用sigmoid激活函数，输出层有2个神经元并使用softmax激活函数的网络，拓扑如下：

# construct the network

# input layer: 4 inputs
# hidden layer: 5 neurons with sigmoid as activate function
# * weight: 4x5 matrices
# * bias: 1x5 matrices
# output layer: 2 neurons with softmax as activate function
# * weight: 5x2 matrices
# * bias: 1x2 matrices

# initialize the weight/bias of the hidden layer (2nd layer)
w2 = np.random.rand(4, 5)
b2 = np.random.rand(1, 5)

# initialize the weight/bias of the output layer (3rd layer) 
w3 = np.random.rand(5, 2)
b3 = np.random.rand(1, 2)
num_epochs = 10000
eta = 0.1

x=[]
y=[]

# training process
for i in xrange(num_epochs):
    # feed forward
    z2 = np.dot(input, w2) + b2
    a2 = sigmoid(z2)

    z3 = np.dot(a2, w3) + b3
    #z3 = np.dot(a2, w3)
    a3 = softmax(z3)

    if i%1000 == 0:
        print "Perception", a3
        print "W2", w2
        print "B2", b2
        print "W3", w3
        print "B3", b3

    x.append(i)
    y.append(cost(a3, output))

    delta_l3 = a3 - output
    deriv_w3 = np.dot(a2.T, delta_l3)
    deriv_b3 = delta_l3
    w3 -= eta*deriv_w3
    b3 -= eta*np.mean(deriv_b3, 0)

    delta_l2 = np.dot(delta_l3, w3.T)*(a2*(1-a2))
    deriv_w2 = np.dot(input.T, delta_l2)
    deriv_b2 = delta_l2
    w2 -= eta*deriv_w2
    b2 -= eta*np.mean(deriv_b2, 0)

完整代码

参考

• http://neuralnetworksanddeeplearning.com/chap3.html#softmax
• https://zhuanlan.zhihu.com/p/25723112
• http://colah.github.io/posts/2015-09-Visual-Information/