数学期望、方差、标准差、协方差
最近在学习机器学习的过程中发现了许多上学时在概率论和统计学课上学过的知识点,可是年代久远已经都忘记了,重新学起来还是费了不少力气,不过因为带着目的学习所以也有了一些新的认识。
数学期望(mean)
概率论中描述一个随机事件中的随机变量的平均值的大小可以使用“数学期望”(mean)这个概念。
数学期望的定义是实验中每次可能的结果的概率乘以其结果的总和。
离散型随机量的数学期望
定义:离散型随机变量的所有可能取值 $ x_i $ 与其对应的概率 $ P( x_i ) $ 乘积的和为该离散型随机量的数学期望,记为 $ E(X) $。
公式:$$ E(X) = \sum_{i=1}^n x_i P_i$$
连续型随机量的数学期望
定义:假设连续型随机变量 $ X $ 的概率密度函数为 $ f(x) $ ,如果积分 $ \int_{-\infty}^{+\infty} xf(x) \,{\rm d}x $ 绝对收敛,则称这个积分的值为连续型随机量的数学期望,记为 $ E(X) $。
公式:$$ E(X) = \int_{-\infty}^{+\infty} xf(x) \,{\rm d}x $$
数学期望的性质
- 设C为常数: $ E(C) = C $
- 设C为常数: $ E(CX) = CE(X) $
- 加法:$ E(X+Y) = E(X) + E(Y) $
- 当X和Y相互独立时,$ E(XY) = E(X)E(Y) $ (主意,X和Y的相互独立性可以通过下面的“协方差”描述)
数学期望的意义
根据根据“大数定律”的描述,这个数字的意义是指随着重复次数接近无穷大时,数值的算术平均值几乎肯定收敛于数学期望值,也就是说数学期望值可以用于预测一个随机事件的平均预期情况。
均值
在往下面的内容走之前说一个简单的概念“均值”,就是平均数。
定义: 给定一个包含n个样本的集合 X={X1, …Xn},均值就是这个集合中所有元素和的平均值。
公式: $ \overline X = {{\sum_{i=1}^n X_i } \over {n}} $
方差(Variance)
方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量,换句话说如果想知道一组数据之间的分散程度的话就可以使用“方差”来表示了。
方差有两个定义,一个是统计学的定义,一个是概率论的定义。
统计学方差
定义:在统计描述中,方差用来计算每一个变量(观察值)与总体均数之间的差异。为避免出现离均差总和为零,离均差平方和受样本含量的影响,统计学采用平均离均差平方和来描述变量的变异程度。
公式:
$$ \sigma^2 = {\sum_{i=1}^N(X-\mu)^2 \over N} $$
其中 $ \sigma^2 $ 为总体方差,X为变量,$ \mu $ 为整体均值, N为总体例数。
样本方差
由于在实际环境里是没有办法穷举所有例子,所以只能找出部分的样本数据,基于这部分样本进行测算。那么可以把公式转换成:
$$ S^2 = {{\sum_{i=1}^n(X_i - \overline X)}^2 \over (n - 1)} $$
其中 $ S^2 $ 为样本方差, $ \overline X $ 是采集样本的均值,$ n $ 为样本的个数。
概率论方差
在概率分布中,设X是一个离散型随机变量
定义:在概率分布中,设X是一个离散型随机变量,若 $ E((X-E(X))^2) $ 存在,则称 $ E((X-E(X))^2) $ 为X的方差,记为 $ D(X) $ , $ Var(X) $ 或 $ DX $,其中 $ E(X) $ 是X的期望值,X是变量值,公式中的 $ E $ 是期望值expected value的缩写,意为“变量值与其期望值之差的平方和”的期望值。
离散型随机变量方差计算公式:
$$ D(X) = E((X-E(X))^2) = E(X^2) - (E(X))^2 $$
- 连续性变量X,若其定义域为 $ (a,b) $,概率密度函数为 $ f(x) $,连续型随机变量X方差计算公式:
$$ D(X) = \int_a^b (x - \mu)^2f(x) \,{\rm d}x $$
方差的意义
那么什么是分散程度呢?举个例子,比如说两个人在游乐场里玩射击游戏时打出了n发子弹,这些子弹有写离靶心近一些,有的远一些,但统计下来这两个人的得分可能相同,这时候如何区分这两个人的水平高低呢?比较直观的一个想法就是看谁的射击弹着点比较集中啦。
标准差(Standard Deviation)
定义:又叫均方差,是离均差平方的算术平均数的平方根,用$ \sigma $ 表示。标准差是”方差”的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
公式:
$$ \sigma = \sqrt 方差 = \sqrt {\sum_{i=1}^N(X-\mu)^2 \over N} $$
样本标准差
类似样本方差,在实际情况中很难知道所有的情况只能靠抽样来估算实际的标准差。
$$ S = \sqrt 样本方差 = \sqrt {{{\sum_{i=1}^n(X_i - \overline X)}^2 \over (n - 1)}} $$
意义
标准差和方差一样都是用于衡量样本的离散程度的量,那么为什么要有标准差呢?因为方差和样本的“量纲”不一样,换句话说不在一个层次。怎么理解这个层次呢,从公式看方差是样本与均值的差的平方和的平均,这里有一个平方运算,这是导致量纲不在同一个层次的原因。
比如两个集合 $ [0,8,12,20] $ 和 $ [8,9,11,12] $ ,两个集合的均值都是10,两个集合的方差分别是:69.33和3.33;计算两者的标准差分别是:8.3和1.8。数字越大代表越离散,从数值上看方差和标准差的量纲差别就很明显了,而标准差更好的在量纲上与样本集合保持同步。这就是“标准”的意义了。
协方差(Covariance)
前面的方差/标准差描述的是一维数据集合的离散程度,但世界上的现象普遍是多维度数据描述的。那么很自然就会想知道现象和数据的相关程度,以及各维度数据间的相关程度。
比如,一个产品卖的好不好可能有很多因素构成,比如产品质量、价格等。那么是否质量和价格之间有相关性呢?这个问题就可以用协方差来解决。
概率论协方差
- 公式:期望值分别为 $ E(X) $ 和 $ E(Y) $ 的两个变量X和Y的协方差为:
$$ Cov(X,Y) = E[(X-E(X))(Y-E(Y))] $$
$$ = E(XY)- 2E(X)E(Y) + E(X)E(Y) $$
$$ = E(XY)- E(X)E(Y) $$
协方差表示的是两个变量的总体的误差,这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X 与Y 是统计独立的,那么二者之间的协方差就是0,则:
$ E(XY) = E(X)E(Y) $
统计学样本协方差
对于包含两个随机变量关系的统计量,我们可以仿照方差的定义:
- 公式:
$$ cov(X,Y) = {{\sum_{i=1}^n (X_i - \overline X)(Y_i - \overline Y)} \over (n-1)} $$
注:从协方差公式可以看出“方差”是协方差在 $ Y=X $ 时的特殊情况。
协方差性质
- 同一个变量的协方差等于其方差:$ Cov(X, X) = Var(X) $
- $ Cov(aX, bY) = ab Cov(X, Y) $ (a, b为常量)
- $ Cov(X_1 + X_2, Y) = Cov(X_1, Y) + Cov(X_2, Y) $
相关系数 (Correlation)
协方差作为描述X和Y相关程度的量,在同一物理量纲之下有一定的作用,但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念:
$$ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} }$$
相关关系
相关性是一个衡量线性独立的无量纲数,其取值在 $ [-1,+1] $ 之间。
- 相关性 η = 1时称为“完全线性相关”,此时将 $ Y_i $ 对 $ X_i $作Y-X 散点图,将得到一组精确置換在直线上的点;相关性数值介于-1到1之间时,其绝对值越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。
- 相关性 η = -1时称为“完全线性负相关”,作图与 η = -1类似也在一条直线上,但方向不同。
- 相关性 η = 0时两个随机变量又被称为是不相关,“线性无关”、“线性不相关”,这仅仅表明X 与Y 两随机变量之间没有线性相关性,并非表示它们之间一定没有任何内在的(非线性)函数关系
协方差矩阵
假设数据集有{x, y, z}三个维度,那么其协方差矩阵为:
其中:
$$ Cov(X,X) = Var(X) $$
$$ Cov(Y,Y) = Var(Y) $$
$$ Cov(Z,Z) = Var(Z) $$
可以看出来协方差矩阵有几个特点:
- 对角线上每个元素的值为方差
- 协方差矩阵是对称矩阵
怎么理解协方差矩阵的意义呢?假设我们在做一项数据分析,每一项数据包含若干指标,那么协方差矩阵的对角线上的每一项可以告诉我们收集数据的分散程度,其它项综合起来可以用前面的相关性方程 $ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} }$ 计算出指标间的相互影响关系。
正相关:
import numpy as np
import matplotlib.pyplot as plt
x, y = np.random.multivariate_normal([0, 0], [[1, 0.9], [0.9, 1]], 1000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()
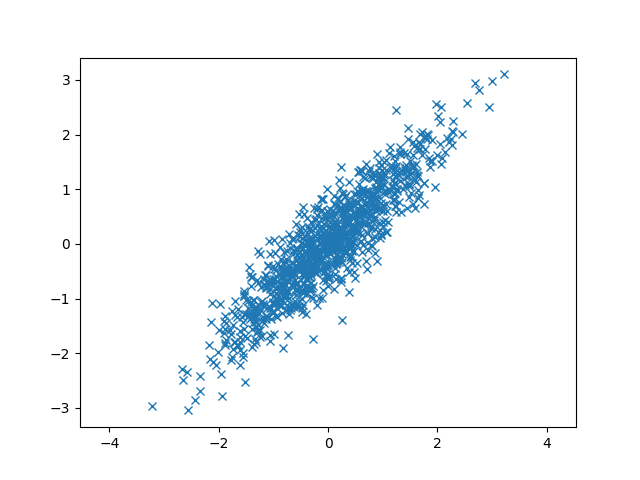
从图中可以看出来x和y之间的关系是一个变大的同时另一个也变大,这说明x和y是正相关,$ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} } = { 0.9 \over \sqrt {1*1}} = 0.9 > 0 $ 也说明了这一点。
指标x的方差$ Cov(x,x) = 1 $和y的方差 $ Cov(y,y) = 1 $说明数据分散不太严重,这一点可以从数据点分散的坐标范围看出来。
分散正相关
import numpy as np
import matplotlib.pyplot as plt
x, y = np.random.multivariate_normal([0, 0], [[5, 4.9], [4.9, 5]], 1000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()
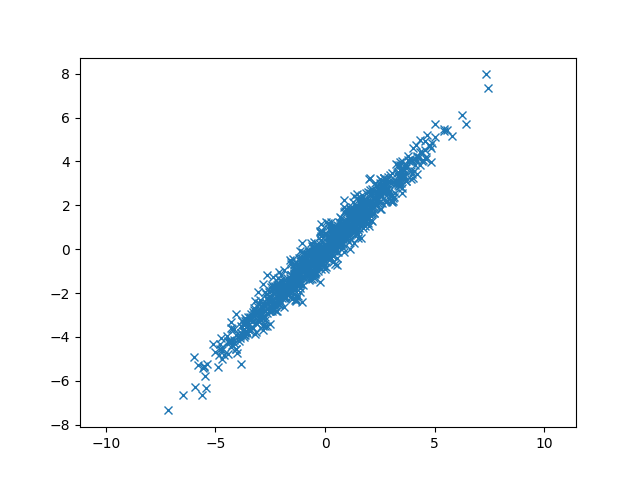
从图中可以看出来x和y之间正相关,并且$ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} } = { 4.9 \over \sqrt {5*5}} = 0.98 > 0 $ 也说明了这一点。
指标x的方差$ Cov(x,x) = 5 $和y的方差 $ Cov(y,y) = 5 $说明数据分散性比前面的例子大了,数据点分散的坐标范围比前面的大了。
分散负相关:
import numpy as np
import matplotlib.pyplot as plt
x, y = np.random.multivariate_normal([0, 0], [[5, -4.9], [-4.9, 5]], 1000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()
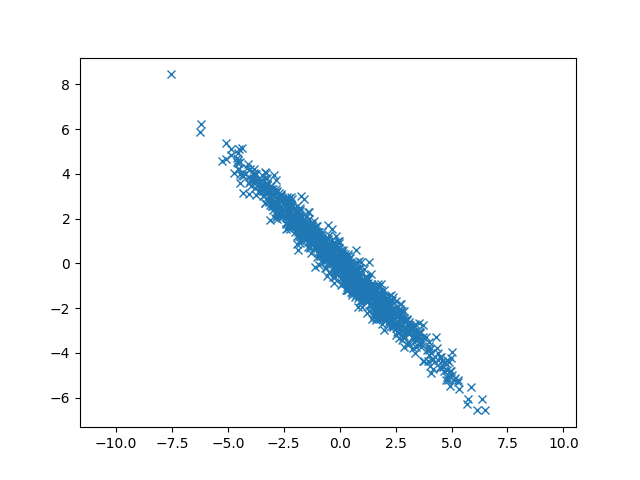
从图中可以看出来x和y之间负相关,并且$ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} } = { -4.9 \over \sqrt {5*5}} = -0.98 < 0 $ 也说明了这一点。
指标x的方差$ Cov(x,x) = 5 $和y的方差 $ Cov(y,y) = 5 $说明数据分散性比前面的例子大了,数据点分散的坐标范围比前面的大了。
分散不相关:
import numpy as np
import matplotlib.pyplot as plt
x, y = np.random.multivariate_normal([0, 0], [[5, 0.1], [0.1, 5]], 1000).T
plt.plot(x, y, 'x')
plt.axis('equal')
plt.show()
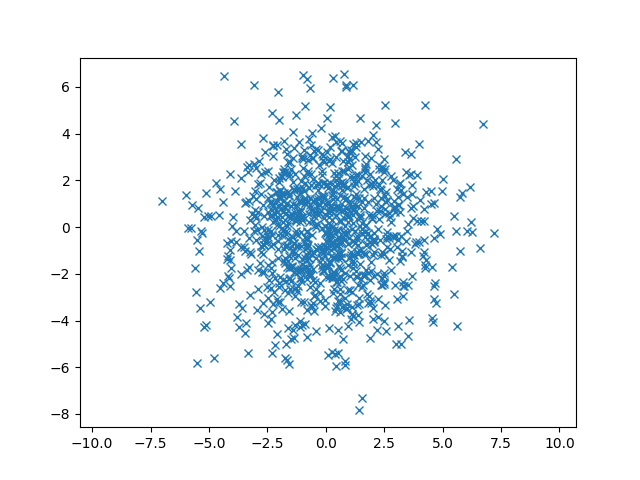
从图中可以看出来每个点都比较分散而且点与点之间没有明显的关系,并且$ \eta = Corr(X, Y) = {Cov(X, Y) \over \sqrt {Var(X) \cdot Var(Y)} } = { 0.1 \over \sqrt {5*5}} = 0.02 \approx 0 $ 也说明了这一点。
指标x的方差$ Cov(x,x) = 5 $和y的方差 $ Cov(y,y) = 5 $说明数据分散性比前面的例子大了,数据点分散的坐标范围比前面的大了。
参考
https://baike.baidu.com/item/数学期望
https://baike.baidu.com/item/方差
